Gamma Function Facts For Kids
The Gamma Function is a mathematical function that extends the concept of factorial to complex and non-integer numbers, helping in many areas of math like calculus and statistics.
Do more with AI
Introduction
The gamma function is a special math tool that helps us understand numbers better. Itโs like a superhero version of the regular factorial function! ๐คฉWhile the factorial only works with whole numbers (like 3! = 3 ร 2 ร 1 = 6), the gamma function can work with many more types of numbers, including fractions and complex numbers. It was created by a brilliant mathematician named Leonhard Euler in the 18th century. ๐The gamma function is used in various fields like physics and statistics. So, letโs dive in and learn more about this amazing math treasure! ๐
Images of Gamma Function
ฮ ( x + 1 ) {displaystyle Gamma (x+1)} interpolates the factorial function to non-integer values.
The gamma function, ฮ(z) in blue, plotted along with ฮ(z) + sin(ฯz) in green. Notice the intersection at positive integers. Both are valid extensions of the factorials to a meromorphic function on the complex plane.
Absolute value (vertical) and argument (color) of the gamma function on the complex plane
Colors showing the argument of the gamma function in the complex plane from โ2 โ 2i to 6 + 2i
Representation of the gamma function in the complex plane. Each point z {displaystyle z} is colored according to the argument of ฮ ( z ) {displaystyle Gamma (z)} . The contour plot of the modulus | ฮ ( z ) | {displaystyle |Gamma (z)|} is also displayed.
3-dimensional plot of the absolute value of the complex gamma function
The analytic function logฮ(z)
Logarithmic gamma function in the complex planefrom โ2 โ 2i to 2 + 2i with colors
Comparison of the gamma function (blue line) with the factorial (blue dots) and Stirling's approximation (red line)
Daniel Bernoulli's letter to Christian Goldbach (Oct 6, 1729)
ฮ ( x + 1 ) {\displaystyle \Gamma (x+1)} interpolates the factorial function to non-integer values.
The gamma function, ฮ(z) in blue, plotted along with ฮ(z) + sin(ฯz) in green. Notice the intersection at positive integers. Both are valid extensions of the factorials to a meromorphic function on the complex plane.
Absolute value (vertical) and argument (color) of the gamma function on the complex plane
Colors showing the argument of the gamma function in the complex plane from โ2 โ 2i to 6 + 2i
Representation of the gamma function in the complex plane. Each point z {\displaystyle z} is colored according to the argument of ฮ ( z ) {\displaystyle \Gamma (z)} . The contour plot of the modulus | ฮ ( z ) | {\displaystyle |\Gamma (z)|} is also displayed.
3-dimensional plot of the absolute value of the complex gamma function
The analytic function logฮ(z)
Logarithmic gamma function in the complex planefrom โ2 โ 2i to 2 + 2i with colors
Comparison of the gamma function (blue line) with the factorial (blue dots) and Stirling's approximation (red line)
Daniel Bernoulli's letter to Christian Goldbach (Oct 6, 1729)
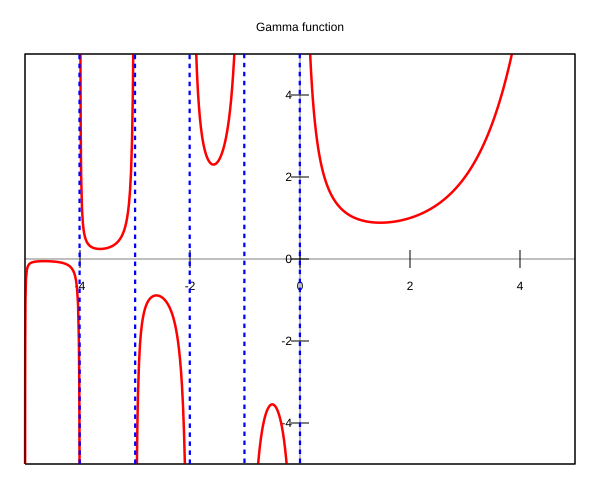
Visualization And Graphs
Visualizing the gamma function helps us understand it better! ๐If you were to draw a graph of the gamma function, it would look like a smooth curve starting at 0 and rising as you move right. The graph has some interesting "humps" and "dips" showing how the gamma value changes for different numbers. ๐คThese patterns can also indicate how gamma interacts with other mathematical functions. You can even see the difference in behavior between whole numbers and fractions! Graphing it out helps us visualize those numbers better! ๐
Applications In Mathematics
The gamma function has many exciting uses in mathematics! ๐It shows up in various areas like calculus, statistics, and even number theory. For example, mathematicians use it to solve difficult problems involving probability and distributions. ๐Moreover, the gamma function is key in calculating things like the area under curves! Itโs also used in physics to solve equations involving energy and particles. This makes the gamma function an essential tool for scientists exploring the universe! ๐Isnโt it fun to see math everywhere in real life?
Relationship With Factorials
The gamma function connects beautifully to factorials! ๐If you take any whole number n, the gamma function gives you the factorial of that number minus one. For example, ฮ(4) = 3! = 6, because 3! = 3 ร 2 ร 1 = 6. ๐So, the gamma function can be viewed as an extension of the factorial function. That means whenever you need to calculate factorials, you can also use the gamma function to do it faster! Isnโt it amazing how one idea leads to another in math? ๐ซ
Extensions And Generalizations
Math is a never-ending adventure! ๐The gamma function has led to lots of extensions and generalizations. One exciting generalization is called the "Beta function," which relates to the gamma function and allows mathematicians to solve even broader problems! Another extension includes rules for calculating the gamma function with negative numbers and fractions using special techniques. ๐Itโs like a family of functions that grow together! These extensions help mathematicians explore new ideas and solve problems that seemed impossible before! How wonderful is that? ๐
Definition Of The Gamma Function
The gamma function is usually written as ฮ(n). Itโs defined for numbers greater than zero and can be thought of as a way to find "factorials" for all numbers. For example, for a whole number n, ฮ(n) = (n-1)!, which means โn minus one, factorial.โ ๐ค If you want to use it with fractions or decimals, we can calculate it for numbers like 2.5 or 3.7! Isnโt that cool? ๐This function is really helpful in math because it also fills in the 'gaps' between whole numbers, making it more versatile!
Properties Of The Gamma Function
The gamma function has some neat properties that make it special! Firstly, it has a property called โrecursionโ that lets us calculate ฮ(n) using the previous value. For example, ฮ(n) = (n - 1) ร ฮ(n - 1). This means we can keep finding values by using previous ones! ๐Also, ฮ(1) = 1 and ฮ(2) = 1. These values are super important! The gamma function is always positive for positive numbers, and it is defined for complex numbers too. ๐These properties make it a valuable tool for mathematicians!
Gamma Function For Complex Numbers
The gamma function isnโt just for whole numbers but is also super helpful for complex numbers! ๐Complex numbers are special because they have a part that is โrealโ (like 2) and a part that is โimaginaryโ (like 3i). ๐คฏThe gamma function is defined for complex numbers except for negative whole numbers like -1, -2, etc. This means you can explore even more numbers in mathematics! The gamma function helps scientists and engineers work with these complex numbers in cool ways, like in physics or computer graphics!
Special Values Of The Gamma Function
Some values of the gamma function are particularly interesting! ๐For example, ฮ(1) = 1, and ฮ(2) = 1. These are special because they establish the beginning points for calculating other values. Additionally, there are some fractions, too! ฮ(1/2) = โฯ (which is about 1.772)! This helps mathematicians relate concepts in geometry and probability. Another notable value is ฮ(3) = 2, which is simply 2! The gamma function's special values can help unlock hidden math secrets! ๐
Integral Representations Of The Gamma Function
If you want to calculate the gamma function, thereโs a cool way to represent it using an integral! ๐An integral is like adding up tiny bits to find a total. The formula for the gamma function is: ฮ(n) = โซ from 0 to โ (x^(n-1) * e^(-x) dx), where e is a special number (about 2.718). This integral shows how gamma relates to calculating areas under curves. Itโs a powerful tool in math that helps explain complex ideas with simple shapes like curves! ๐ข
Gamma Function Quiz
Learn more about Gamma Function
