Facts for Kids
Eccentricity is a special number that tells us how different a conic section is from a perfect circle, helping to understand shapes like circles, ellipses, and hyperbolas.
Overview
Types Of Conic Sections
Eccentricity In Astronomy
Definition Of Eccentricity
Related Concepts In Geometry
Mathematical Formula For Eccentricity
Common Misconceptions About Eccentricity
Eccentricity And Shape Of Conic Sections
Applications Of Eccentricity In Real Life
Graphing Conic Sections Based On Eccentricity
Historical Context Of Eccentricity In Geometry
Inside this Article
Apollonius Of Perga
Conic Section
Real Number
Astronomy
Equation
Geometry
Concept
Ellipse
Circle
Sun
Are
Did you know?
๐ต Eccentricity is a number that tells us how 'stretchy' or 'squished' a shape is.
๐ A circle has an eccentricity of 0, making it perfectly round!
๐ An ellipse has an eccentricity between 0 and 1, showing it's stretched out.
๐ A parabola has an eccentricity of exactly 1, which gives it a unique 'U' shape.
๐ Hyperbolas have an eccentricity greater than 1, indicating they are very stretched.
๐ The formula for eccentricity can change depending on the shape we are measuring!
โ๏ธ Conic sections are produced by slicing through a cone, which is why they're called that.
๐ก All conic sections โ circle, ellipse, parabola, and hyperbola โ have different shapes.
๐ Eccentricity is important in real life, like how planets orbit the sun!
๐ The concept of eccentricity has been studied since ancient Greece by famous mathematicians.
Introduction
It tells us how "stretchy" or "squished" a shape is, especially when we look at cones, circles, and other curved lines called conic sections. For example, a circle has low eccentricity because itโs very round, while an oval has higher eccentricity since itโs stretched out. ๐
So, eccentricity is like a special number that helps us know how different shapes look!
Types Of Conic Sections
A circle has a constant distance from the center, while an ellipse looks like a stretched circle. A parabola looks like a "U" shape and can come in two directions. A hyperbola has two "arms" that go outwards away from each other. These shapes are formed by slicing through a cone, which is why theyโre called conic sections! ๐บโ๏ธ
Eccentricity In Astronomy
For example, Earth has an eccentricity of about 0.0167, making its orbit almost a perfect circle. But comets often have high eccentricity, meaning they travel long, stretched paths around the sun. ๐
This changes how often we see them. Eccentricity is important for scientists studying space and predicting when different objects will appear in the sky!
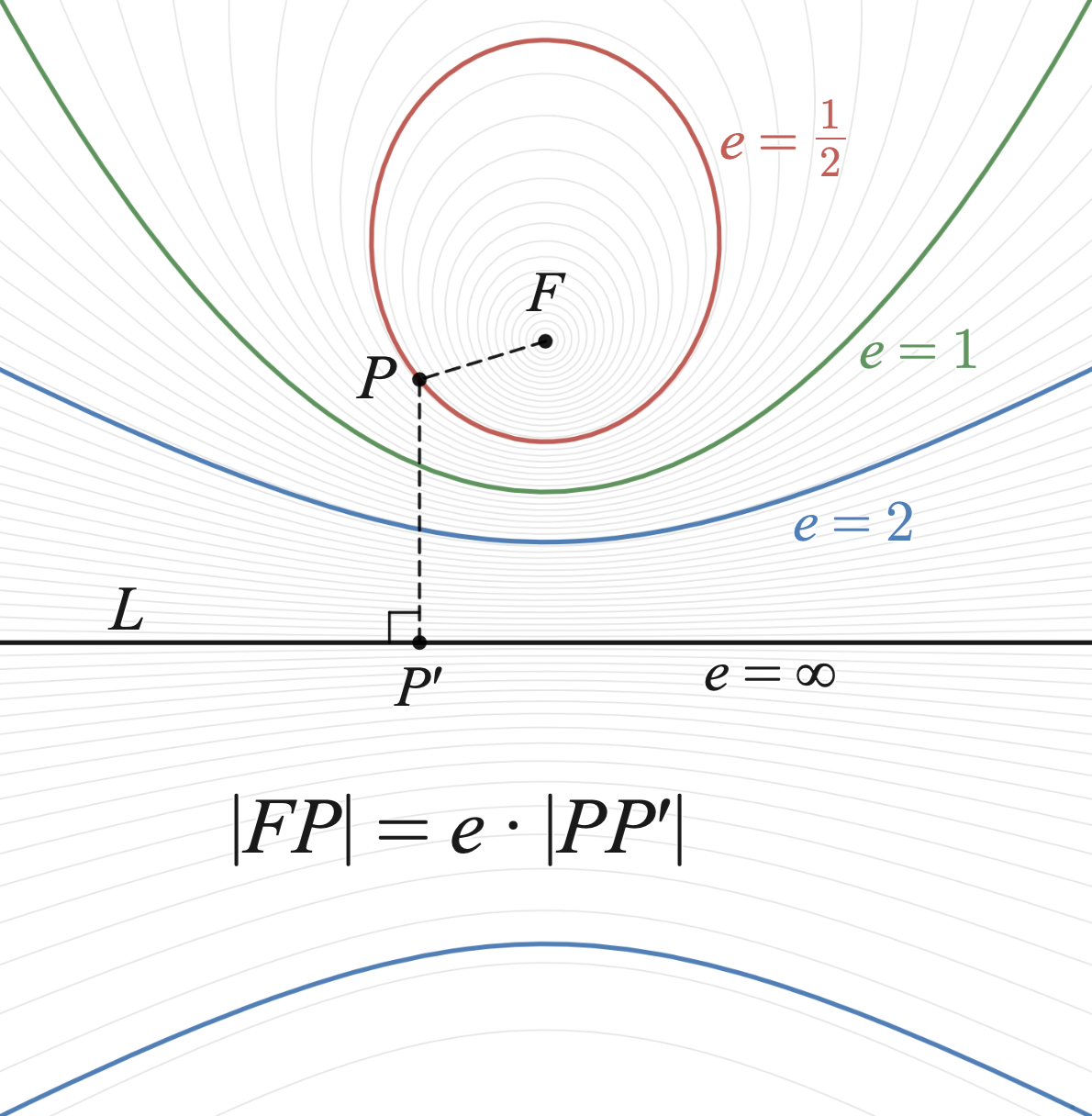
Definition Of Eccentricity
In math, we often use the letter "e" to represent eccentricity. The key thing to know is: if e = 0, itโs a circle! If e is between 0 and 1, we have an oval (ellipse). But when e is 1, we find a special shape called a parabola. And for e greater than 1, we have a shape called a hyperbola! ๐
Related Concepts In Geometry
For example, the focus and directrix are two key points related to conic sections and help define shapes like parabolas. We also have the terms "vertex" and "axis of symmetry," which relate to how conic sections look on a graph! By learning about eccentricity, kids can also explore other geometric concepts, creating a big exciting world of shapes and numbers! ๐
Mathematical Formula For Eccentricity
For parabolas, e is always equal to 1, while for hyperbolas, e = โ(1 + (bยฒ/aยฒ)). All these formulas help mathematicians measure the "stretch" of the shape!
Common Misconceptions About Eccentricity
Eccentricity And Shape Of Conic Sections
A circle is perfectly round, so its eccentricity is 0! As we move to an ellipse, its eccentricity tells us how oval it is: the more it stretches, the closer that number gets to 1. For a parabola, e is exactly 1, making it unique. Lastly, hyperbolas, which look like two curves, have eccentricity greater than 1 showing they are very stretched out! ๐
Applications Of Eccentricity In Real Life
For example, in astronomy, planets follow elliptical orbits around the sun, meaning they have a little eccentricity. This affects how fast they move! Eccentricity also helps engineers design roller coasters that twist and turn just right! ๐ข
Even in architecture, it guides curves in bridges and buildings. So, eccentricity is helping us make cool things all over the world!
Graphing Conic Sections Based On Eccentricity
For circles (e=0), we draw a perfect round shape. To make an ellipse (e between 0 and 1), we stretch our circle a little. For parabolas (e=1), we create a โUโ shape that opens either up or down. Hyperbolas are trickier! We need to make two arms that separate, showing greater eccentricity (e>1). Using equations, we can turn these ideas into pretty pictures on a graph! ๐จ
Historical Context Of Eccentricity In Geometry
The famous mathematician conic sections was used and studied by great minds like Apollonius of Perga around 200 BC! Over time, mathematicians like Johannes Kepler and Sir Isaac Newton continued exploring these shapes. Their discoveries helped us understand not only geometry but also the orbits of planets! ๐
Thanks to their work, we now enjoy the benefits of eccentricity in both math and science!
Eccentricity Quiz
Frequently Asked Questions
Our Mission
To create a safe space for kid creators worldwide!
2025, URSOR LIMITED. All rights reserved. DIY is in no way affiliated with Minecraftโข, Mojang, Microsoft, Robloxโข or YouTube. LEGOยฎ is a trademark of the LEGOยฎ Group which does not sponsor, endorse or authorize this website or event. Made with love in San Francisco.